Solve a 1D wave equation with absorbing boundary conditions.
Specify a wave equation with absorbing boundary conditions. Note that the Neumann value is for the first time derivative of :
u
In[170]:=
eqn=D[u[t,x],{t,2}]D[u[t,x],{x,2}]+NeumannValue[-Derivative[1,0][u][t,x],x0||x1];
Specify initial conditions for the wave equation:
In[171]:=
u0[x_]:=Evaluate[D[0.125Erf[(x-0.5)/0.125],x]];ic={u[0,x]u0[x],Derivative[1,0][u][0,x]0};
Solve the equation using the finite element method:
In[173]:=
ufun=NDSolveValue[{eqn,ic},u,{t,0,1},{x,0,1},Method{"MethodOfLines","SpatialDiscretization"{"FiniteElement"}}];
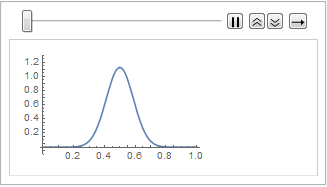
Visualize the wave equation with absorbing boundary conditions:
In[12]:=
list=Table[Plot[ufun[t,x],{x,0,1},PlotRange{-0.1,1.3}],{t,0,1,0.1}];ListAnimate[list]
absorbing_conditions.swf